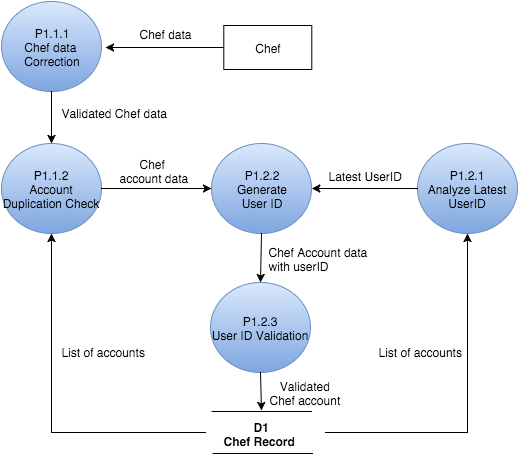
- DFD, Data Flow Diagram
- 자료의 흐름 및 변환 과정과 기능을 도식화하여 기술하는 요구사항 분석 기법
- 럼바우 분석 기법 중 기능 모델링에 해당한다.
- 버블 차트(Bubble chart)라고도 한다.
작성 5단계
- 자료 흐름 유형확정
- 자료 흐름 경계 표시
- DFD를 프로그램 구조로 사상
- 제어 계층을 분해시켜서 정의
- 결과 구조는 설계측정들과 경험적 학습법을 사용해서 정제
작성 원칙
- 자료 보존의 법칙(Conservation Rule)
- 출력 자료 흐름은 반드시 입력 자료 흐름을 이용해 생성
- 최소 자료의 원칙(Parsimony Rule)
- 출력 자료를 산출하는데 필요한 최소의 자료 흐름만 표현
- 독립성의 원칙(Independence Rule)
- 프로세스는 자신의 자료 입출력에 대해서만 인지
- 지속성의 원칙(Persistence Rule)
- 프로세스는 항상 수행되고 있음
- 순차 처리의 원칙(Ordering Rule)
- 입력 자료흐름의 순서는 출력 자료흐름에서도 지켜져야 함
- 영구성의 원칙(Permanence Rule)
- 자료저장소의 자료는 입력으로 사용해도 제거되지 않음
- 자료 변환의 원칙(Nature of Change)
- 자료 본질의 변환(Change of Nature)
- 자료 합성의 변환(Change of Composition)
- 자료 관점의 변환(Change of Viewpoint)
- 자료 구성의 변환(Change of Organization)
- 기타
- No 'Black Hole': 입력만 있고 출력이 없으면 안된다.
- No 'Miracle': 입력 없이 출력만 있으면 안된다.
- 개체 간의 데이터 흐름이 있어선 안된다.
- 데이터저장소 간의 데이터 흐름이 있어선 안된다.
- 입력 데이터 흐름은 반드시 변환 후 출력 흐름을 전제로 한다.
구성 요소
- 프로세스(Process)
- 동그라미
- 자료를 변환시키는 처리 과정 하나를 나타냄
- 처리/기능/변환 버블이라고도 함
- 자료 흐름(Flow)
- 화살표
- 자료의 이동을 나타냄
- 자료 저장소(Data Store)
- 평행선(아래위만 선이 그어진 사각형)
- 파일, 데이터베이스 등 자료가 저장되는 곳을 나타냄
- 단말(Terminator)
- 사각형
- 시스템과 교신하는 외부 개체
- 데이터의 입출력 주체(사용자 등)
작성 지침
- 자료 흐름(Flow)은 처리(Process)를 거쳐 변환될 때마다 새로운 이름을 부여함
- 처리(Process)가 출력 자료를 산출하기 위해서는 반드시 입력 자료가 발생해야 함
- 처리(Process)와 하위 자료 흐름도의 자료 흐름은 서로 일치돼야 함
- 자료흐름도의 최하위 처리(process)는 소단위명세서를 가짐
- 자료 저장소에 입력 화살표가 있다고 하여 반드시 출력 화살표가 표시될 필요는 없음
특징
- 도형으로 그려지는 그림 중심의 표현이다.
- 다차원적(Multidimensional)이다.
- 데이터(자료)의 흐름에 중심을 두는 분석용 도구이다.
- 제어(Control)의 흐름은 중요시 하지 않는다.
그 외 구성
자료 사전(DD, Data-dictionary)
- 자료, 자료들의 집합, 자료의 흐름, 자료 저장소와 그들간의 관계·범위·단위들을 구체적으로 명시
- 작성 목적
- 조직 속에 있는 다른 사람들에게 특정한 자료 용어가 무엇을 의미하는지를 알림
- 자료에 관한 용어를 정의하고 취합하여 문서로 명확히 함
- 작성 지침
- 갱신하기 쉬워야 한다.
- 이름이 중복되지 않아야 한다.
- 이름으로 정의를 쉽게 찾을 수 있어야 한다.
- 정의하는 방식이 명확해야 한다.
- 사용 기호
- = is composed of
- + and
- () optional
- {}∩ iteration
- [] selection
- | seperator
- @ key field
- * comment
- ** no comment
소단위 명세서(Mini-Spec)
- 최하위 단계 프로세스의 처리절차
- 자료 흐름도에 나타나 있는 처리 항목을 1~2페이지 정도로 절차 표현
- 아래의 기법 사용
- 구조적 언어(Structured Language) : 절제되고 제한된 자연어 형태로 표현
- 의사결정표(Decision Table) : 표 구조로 표현
- 의사결정도(Decision tree) : 트리 구조로 표현